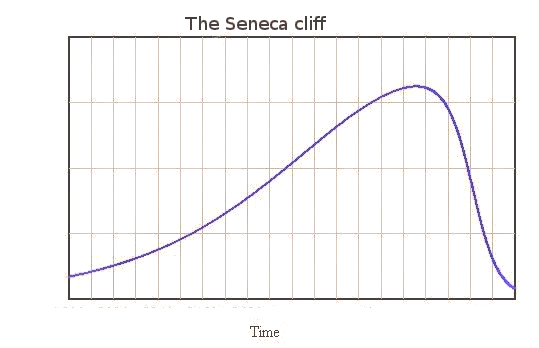
Don't you stumble, sometimes, into something that seems to make a lot of sense, but you can't say exactly why? For a long time, I had in mind the idea that when things start going bad, they tend to go bad fast. We might call this tendency the "Seneca effect" or the "Seneca cliff," from Lucius Annaeus Seneca who wrote that "increases are of sluggish growth, but the way to ruin is rapid."
Could it be that the Seneca cliff is what we are facing, right now? If that is the case, then we are in trouble. With oil production peaking or set to peak soon, it is hard to think that we are going to see a gentle downward slope of the economy. Rather, we may see a decline so fast that we can only call it "collapse." The symptoms are all there, but how to prove that it is what is really in store for us? It is not enough to quote a Roman philosopher who lived two thousand years ago. We need to understand what factors might lead us to fall much faster than we have been growing so far. For that, we need to make a model and see how the various elements of the economic system may interact with each other to generate collapse.
I have been working on this idea for quite a while and now I think I can make such a model. This is what the rest of this post will be about. We'll see that a Seneca cliff may indeed be part of our future if we keep acting as we have been acting so far (and as we probably will). But let's go into the details.
Models of growth and decline
The paradigm of all models of growth and decline is the Hubbert model. Here is how it appeared for the first time, ina paper published by Marion King Hubbert in 1956 where he showed his prediction for crude oil production in the 48 US lower states.
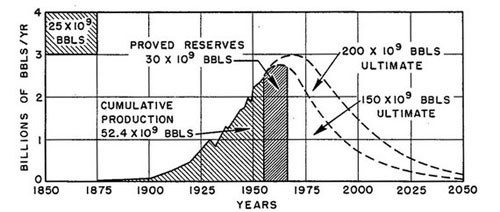
If you are interested in this subject, you probably have seen this plot many times and you also know that it worked nicely as a prediction. Oil production in the US did peak when Hubbert had said it would, in 1970. The Hubbert model has been shown to be a good description of many historical cases of oil producing regions, as reported, for instance, by Adam Brandt in his 2007 paper "Testing Hubbert". It works not just for oil, also for other mineral resources and for slowly renewable biological resources, such as whales (Bardi 2007).
We can take the Hubbert model as a first step for the description of an economic system based on the exploitation of a non renewable resource. The idea underlying the model is that exploitation starts with the best, highest return resources. Then, depletion slowly forces the industry to move to lower return resources. Profits fall and the capability of the industry to invest in new extraction falls as a consequence. This slows down growth and, eventually, causes production to decline (Bardi et al. 2010). So, it is a very general model that could describe not just regional cases but whole civilizations. Most of the agrarian civilizations of the past were based on a depletable resource, fertile soil, as I discussed in a post of mine in 2009.
However, the Hubbert model does not generate the Seneca effect. Not only the production curve is normally assumed to be symmetric, but there are several historical cases where it is skewed backwards; something that we could call the "anti-Seneca" effect. The prevalence of these cases in oil production led Brandt (2007) to state that (p. 27) "....there is simply no evidence in the historical data that rates of decline will be generally sharper than rates of increase. This should be taken as comforting news for those concerned about a quick decline in production causing additional disruption beyond that already anticipated for the transition from conventional oil to substitutes for conventional oil."
Fine, but there is a problem. The results reported by Brandt are all for regional cases and it couldn't be otherwise. But, in a regional case, when extraction costs go up, operators simply move to regions where costs are lower. What happens when there is no new region to move to? That is, what happens when you examine the worldwide trend? Do people simply give up extracting, as it is implicitly assumed in the Hubbert model, or do they try harder? And in the latter case, what happens?
Of course, we don't have historical data for the whole cycle of oil production, worldwide. But there exist models which are more sophisticated than the Hubbert model and which can tell us more about worldwide trends. One is the "World3" model used for "The Limits to Growth" study, first published in 1972. The model is based on assumptions not unlike those at the basis of the Hubbert model (see this post of mine comparing the two models), but it considers the world's economy as a whole. Here are the results of the "base case" scenario of the 2004 version.

Here, we clearly see that the curves for food production and industrial production are skewed forward. It is the Seneca effect; something that appears to be a general trend of these models. For an even clearer view of this trend, here is a graph taken from the front cover of the 2004 edition of "The Limits to growth"
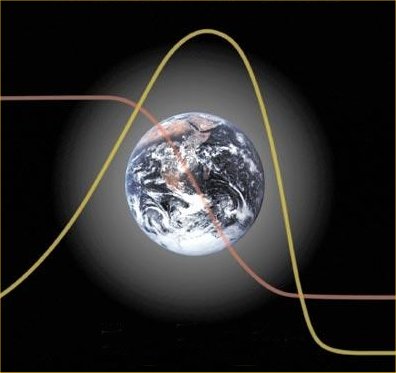
Now, what creates the Seneca effect in a complex model such as "World3" but not in a simpler model as Hubbert's one? In order to understand this point, I'll try now to build simple ("mind sized") world models and see what parameters are the cause of the forward leaning curves. We'll see that the asymmetry is mainly caused by a factor that we may call "pollution."
Mind Sized World Modelling
"Mind Sized" is a term invented by Seymour Papert in his book "Mind Storms" (1980). The idea is that, in order to be convinced that a certain phenomenon is real, or that it may happen for real, you need to understand what makes it real. For this, a model must be simple enough that you can make sense of it within your mind. This was one of the problems with "The Limits to Growth" study of 1972; the model was so complex that people tended to disbelieve its results mostly because they didn't understand how the model worked, as I argue in my book on this subject (Bardi 2011). So, let's see if we can make mind sized world models, trying to explicit their relation with thermodynamics. This was the gist of a talk that I gave in Spain this year, "Entropy, peak oil and stoic philosophy".
For building these models, I'll use "system dynamics," the same method used for "The Limits to Growth" study. It is a method of simulation based on describing systems as composed as "stocks" linked to each other by "flows" controlled by "valves". The classic example of this kind of systems is that of a bathtub. The bathtub is the stock; you can fill it by means of a flow of water, or you can empty it letting water flow out of it. This is called "bathtub dynamics" and you can read a nice paper on this subject by Linda Sweeney and John Sterman. It shouldn't be necessary to say that a bathtub has to obey the laws of physics, but at times it is. You have to remember that mass must be conserved in order to understand how a bathtub fills or drains out. More in general, energy has to be conserved - this is the first law of thermodynamics. You have to remember also the second law of thermodynamics, which says that in everything that happens spontaneously, entropy must increase. Ultimately, the fact that water flows away from the drain of a bathtub has to do with increasing the entropy of the universe.
So, let's try to make a simple, mind-sized model that describes how an economic system exploits a non-renewable resource. We start with a stock that we call "Resources". We assume that it is a stock of energy on the basis of the idea that energy can be transformed into other kinds of resources (say, metals) but not the reverse. The resource could be, for instance "crude oil", which is the main resource on which our civilization is based. Then, we have another box that we call "Capital" that represents energy stocked in forms that can be utilized. We could say that this stock is a section of the economy; say, "the oil industry" or that it represents a whole civilization. Then we draw the flows of energy from the resource stock to the capital stock and to dissipation as low temperature heat, as the second law of thermodynamics commands. Here is the model.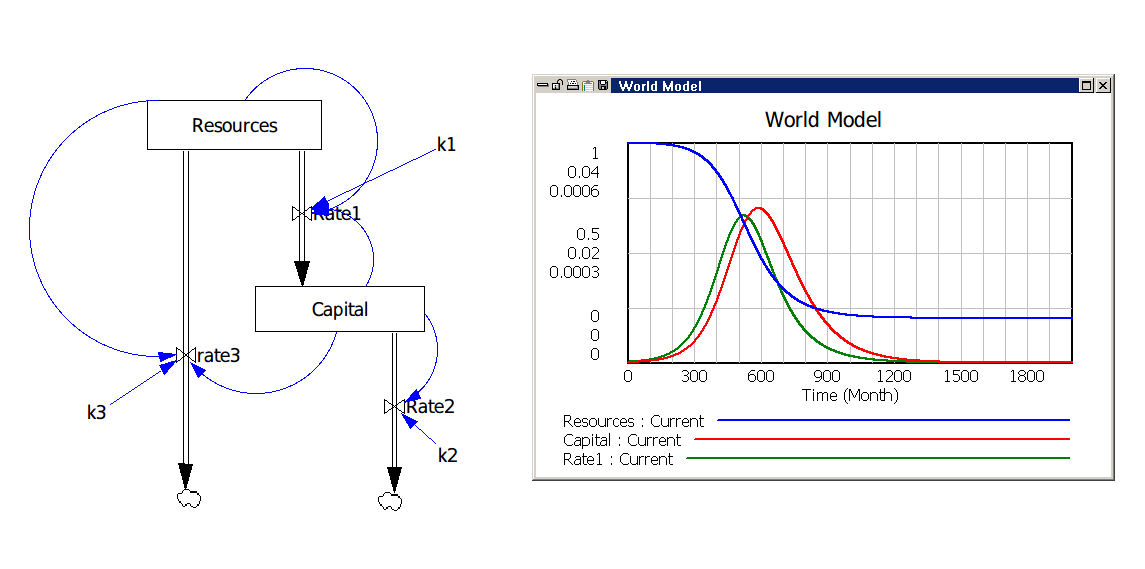
This is the same model that I showed in previous posts (e.g. here) but, here I turned it 90 degrees clockwise in order to emphasize the fact that energy goes "down" from higher thermodynamic potentials to lower thermodynamic potentials; just like what water does in a bathtub or in a fountain. Unlike the case of a fountain or a bathtub, however, here the flow is governed by feedback: resources are transformed into capital in proportion to the amount of both Resources and Capital. Note also that the resource partly decays without producing anything (Rate3). That's due to the inefficiency of the production process; think of oil spills or of natural gas vented and burned.
As you see, the production curve (Rate1 in the figure) is bell shaped and symmetric. This model, indeed, is equivalent to the Hubbert model (Bardi and Lavacchi 2009). The problem is that you can play as much as you like with the model, changing the values of the three constants, but the curves will not show the Seneca effect; that is, decay will not be faster than growth. So, are we missing something, here?
It seems that, indeed, we are missing an element that, instead, is present in the world models of "The Limits to Growth" study. What we are missing is pollution or, better said, the effects of pollution. In the simple model above, degraded energy is harmlessly dissipated to space; it has no effect on the other elements of the model. But we know that, in the real world, that is not true. Pollution has a cost: money and resources must be spent to fight it; be it water or air poisoning or effects such as global warming.
In order to simulate the effects of pollution we can define it as a third stock that drains energy from the capital stock in proportion to the size of both the capital and the pollution stocks. Note that, since there are several constants, I grouped with the name of "l" (from the term "loss") those which go directly from a stock to outer space (l1, l2, l3). I kept the letter "k" for the flows that go from one stock to another. Here is the model. I am showing you a sample output where I chose parameters which emphasize the Seneca effect.

The parameters for this run are k1=0.03. k2=0.3, l1=0, l2=0.01, l3=0.015, Resources (t0)=1, Capital(t0) =0.001, Pollution(t0)=0.001
Here is the production curve, alone, from a different run.
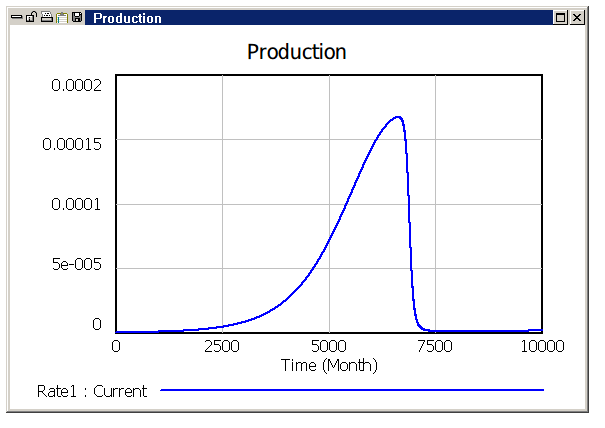
So,the model can generate a "Seneca-like" production curve which clearly shows the "Seneca cliff". It goes up slowly, then it collapses quickly. As Seneca says, "the way to ruin is rapid."
Now, can we say in words what generates the Seneca cliff? Yes, we can. It goes like this: first, consider that the effect of pollution is to drain economic capital. Secondly, consider that the pollution stock grows by feeding on the economy stock - so it has to wait for the economy to have grown before it can grow itself. It is this delay that causes an increase in the rate of energy draining from the economy as the process goes on. Since the size of the economy stock determines the production rate, we see also that parameter going down rapidly after the peak. This is the essence of the Seneca effect.
Let's now go more in depth in the model. What is exactly this "pollution" that causes so much trouble? It is what the authors of "The Limits to Growth" called "persistent pollution" to show that it is something different from infrared radiation harmlessly disappearing into space. It is a very general concept that includes anything that is generated by capital and will drain resources from capital. The Fukushima disaster is a good example of pollution coming back to bite at the industry that produced it. It could be poisoning of the air or of water. It could be global warming and it could also be wars. Wars are great producers of pollution and a nuclear war would make the Seneca effect take place almost instantly.
Now that we understand how the model works, we can go back to to Brandt's study and explain why in the majority of historical cases of oil production the curves are symmetric or show "anti-Seneca" shapes. We said that the Seneca effect is generated by pollution; so, does this result mean that oil extraction produces no pollution? Not at all, of course. It only means that those who extract oil don't have to pay for the pollution they produce. To make a practical example, in the case of oil extraction from the 48 US lower states, persistent pollution has mainly taken the shape of CO2 and other greenhouse gases added to the atmosphere. This is a factor that has not yet bitten us back, but, eventually, someone will have to pay for the damage done in the form of global warming. When the bill comes - and it is coming - we may discover that it is more expensive than what we can afford to pay.
Would technological progress save us from the Seneca cliff? Well, not automatically. Actually, it could make the cliff steeper! One way to simulate technology is to assume that the constants in the model are not constant but vary as the cycle proceeds. For instance, an increasing value of the "k1" constant corresponds to technological improvements in the capability of exploiting the resource. That will increase the total amount produced at the end of the cycle, but will also generate a steeper fall after the peak, as I discussed in a paper of mine (Bardi 2005). A more interesting idea would be to tweak the model by a making the "k2" constant gradually smaller. That would simulate the development of technologies that lower the production of pollution. In other words, the model tells us that "clean production" is a good idea in the sense that it would tend to make the production cycle more symmetric.
You might try other ways to modify the model, for instance increasing its complexity by adding more stocks. How about a "bureaucracy" stock that accumulates and then dissipates energy? Well, it will act just as the "pollution" stock; perhaps we might say that bureaucracy is a form of pollution. Incidentally, anyway, with this added stock the model becomes more similar to Tainter's model that has that civilizations decline and collapse because of an increase in complexity that brings more problems than benefits. If you keep adding more elements to the model, in the end you get to something that may be similar to the "World3" model used in "The Limits to Growth" study. We saw earlier on that this model does generate forward skewed curves.
There are many ways to modify these models and the Seneca effect is not the only possible outcome. Fiddling with the constants you may also generate the opposite behavior; that is the "anti-Seneca" curve, with decline slower than growth. As you would expect, that happens using constants that minimize the accumulation of persistent pollution. But, in general, the Seneca effect is a "robust" feature of this kind of models and it comes up for a variety of assumptions. You ignore the Seneca cliff at your own risk.
The Seneca effect in the real world
Do we have historical examples of the Seneca effect? Well, several, but not many for which we have quantitative data. The Roman civilization, for instance, took about seven centuries to peak and just about three centuries to fall, at least in its Western side (and Seneca himself may have perceived the Roman decline at his time). However, the data we have on such parameters as the Roman population are not good enough to see the effect in the form of a forward skewed curve.
We seem to have such data, instead, for the Mayan civilization. Here is an image taken from Dunning et al (1998). The horizontal scale is very long: 10.000 years from the Pleistocene/holocene boundary.
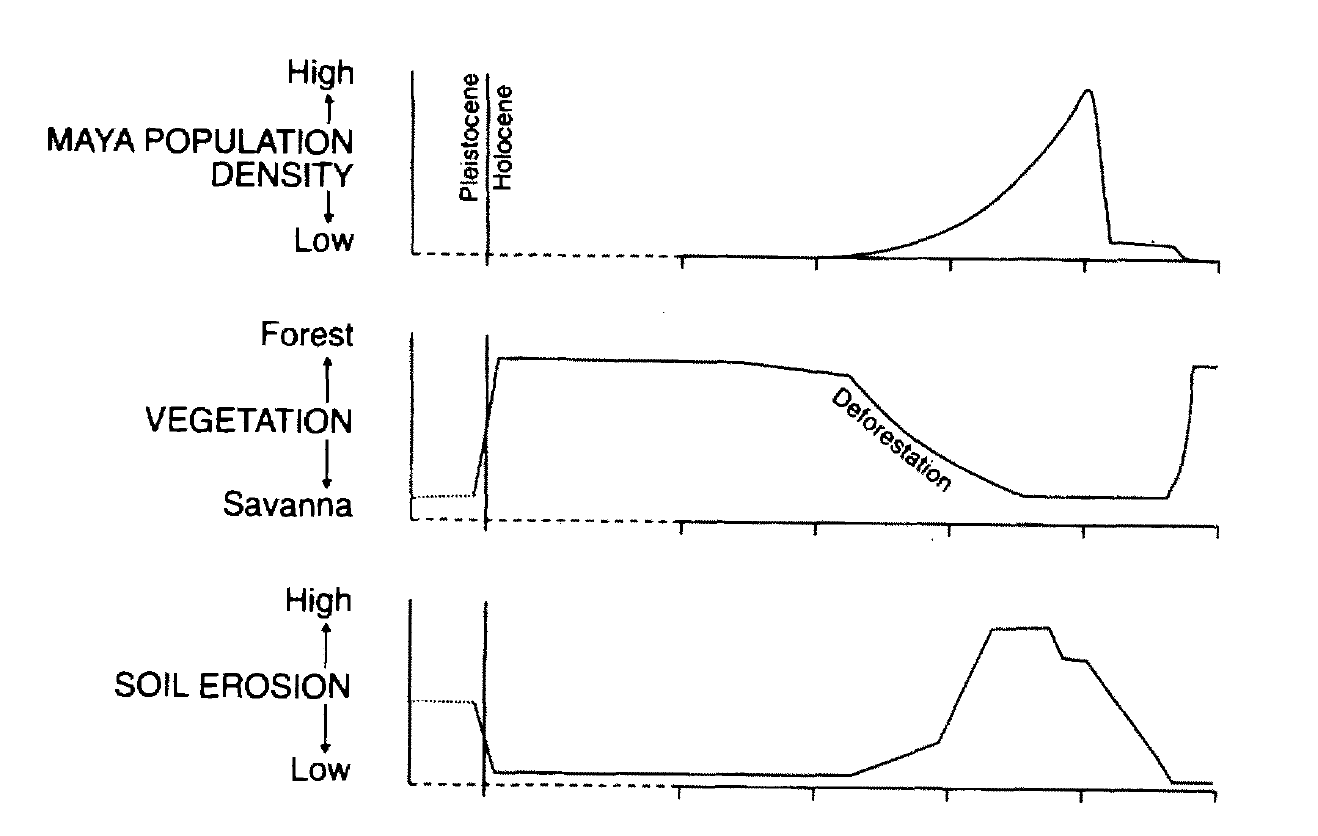
In this case, pollution takes the shape of soil erosion that drains capital resources and generates population collapse. We should be careful with this interpretation, because some authors believe that the Mayan collapse was caused by climate change. But the world model developed here seems to be compatible with the historical data.
For something closer to us, here is a figure taken from Dmitry Orlov's paper "Peak oil is history". It shows Russian oil production.
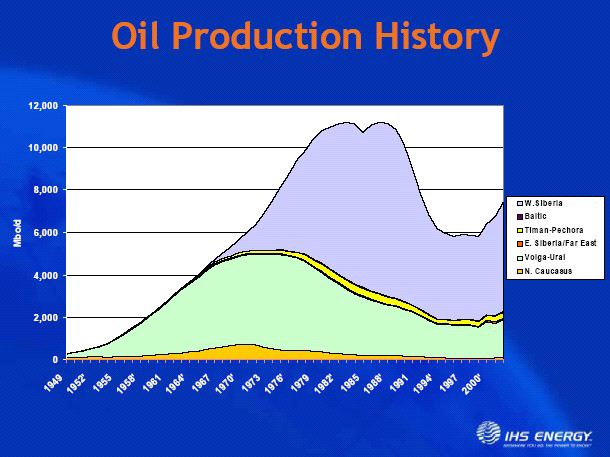
The Soviet Union was a nearly closed economy before collapsing; a "mini-world" in itself. Notice how Russian oil production went down rapidly after the peak; a classic Seneca cliff. Note also how production picked up again afterwards. At some point, the Soviet Union ceased to exist as an isolated economic system and it became part of the whole world's economic system. At that point, the simple model that we have been using does not work any longer; most likely because the capital stock received an influx of resources that came from a region outside the model.
Conclusion: a banquet of consequences
Very often, we fail to understand the delayed effects of our actions. John Sterman reminds us of this point in a talkon global warming quoting Robert Louis Stevenson as saying, "Everybody, sooner or later, sits down to a banquet of consequences." The models shown here tell us that the Seneca cliff is the result of delayed consequences.
As always, the future is something that we build with our actions and the models can only tell us what kind of actions will lead us, eventually, to a certain outcome. Used in this way, models can be extremely useful and can even be applied to systems which are much more modest than an entire civilization, for instance to a single company or to our personal relationships with other people. In all cases, the Seneca effect will be the result of trying hard to keep things running as usual. In that way, we may run out faster of the resource that keeps the system running: be it a physical resource or a reserve of goodwill. The way to avoid this outcome may be to let the system run the way it wants, without attempting to force it to go the way we want it to go. In other words we need to take things in life with some stoicism, as Seneca himself would probably have said.
Thinking of the worldwide situation and of the problems involved, global warming and resource depletion, what the models tell us is that the Seneca cliff may be the inevitable result of putting too much strain on already badly depleted natural resources. We should try, instead, to develop alternative stocks of resources such as renewable (or nuclear) energy. At the same time, we should avoid to exploit highly polluting and expensive resources such as tar sands, oil shales, deepwater oil, and, in general, applying the "drill, baby, drill" philosophy. All those strategies are recipes for doom. Unfortunately, these are also examples of exactly what we are doing.
I don't know what Seneca would say if he could see this planet-wide effort we are making in order to put into practice the idea that he expressed in his letter to his friend, Lucilius. I can only imagine that he would take it with some stoicism. Or, maybe, he would comment with what he said in his "De Providentia" "Let Nature deal with matter, which is her own, as she pleases; let us be cheerful and brave in the face of everything, reflecting that it is nothing of our own that perishes."
Thanks to Dmitry Orlov for having been the source of inspiration for this post with his article "Peak Oil is History".
⸐
References
- Bardi, U., 2007, Energy prices and resource depletion: Lessons from the case of whaling in the nineteenth century” Bardi U. Energy Sources, part B- Economics Planning and Policy Volume: 2 Issue: 3 Pages: 297-304
- Bardi, U. and Lavacchi, A., 2009, "A Simple Interpretation of Hubbert’s Model of Resource Exploitation” Energies 2009, 2(3), 646-661; doi:10.3390/en20300646
- Bardi, U. 2011 "The Limits to Growth Revisited", Springer, ISBN 978-1-4419-9415-8
- Bardi, U., Lavacchi, A., Yaxley L., 2011 “Modelling EROEI and net energy in the exploitation of non renewable resources” Ecological Modelling, In Press.
- Brandt, A.R. (2007). Testing Hubbert. Energy Policy, 35(May):3074-3088. DOI: 10.1016/j.enpol.2006.11.004
- Dunning, N., D. Rue, T. Beach, A. Covich, A. Traverse, 1998, "Human - Environment Interactions in a Tropical Watershed: the Paleoecology of Laguna Tamarindito, Guatemala," Journal of Field Archaeology 25 (1998):139-151.